When it comes to improving qubit fidelity, one indirect question is whether one can enhance gate fidelity by “shaping” pulses that are just more complex than simple guassian looking pulses? And the answer is: “let’s have a look at the _DRAG Pulse”!

The actual reason for the interest in the DRAG Pulse is the comment from Joseph Bardin in the video presentation about Google’s Cryo Pulse Modulator:

[21:08] what we realized is that, if we don’t try and do things like drag, we just need a symmetric envelope. Raised cosine or Gaussian– they’re both symmetric. So what we did was we built an array of programmable current sources, and then have the appropriate enabling functions to create this kind of wedding cake shaped current wave form. And so we can program the amplitudes and so forth.

This is Google’s architecture - and it is really smart:

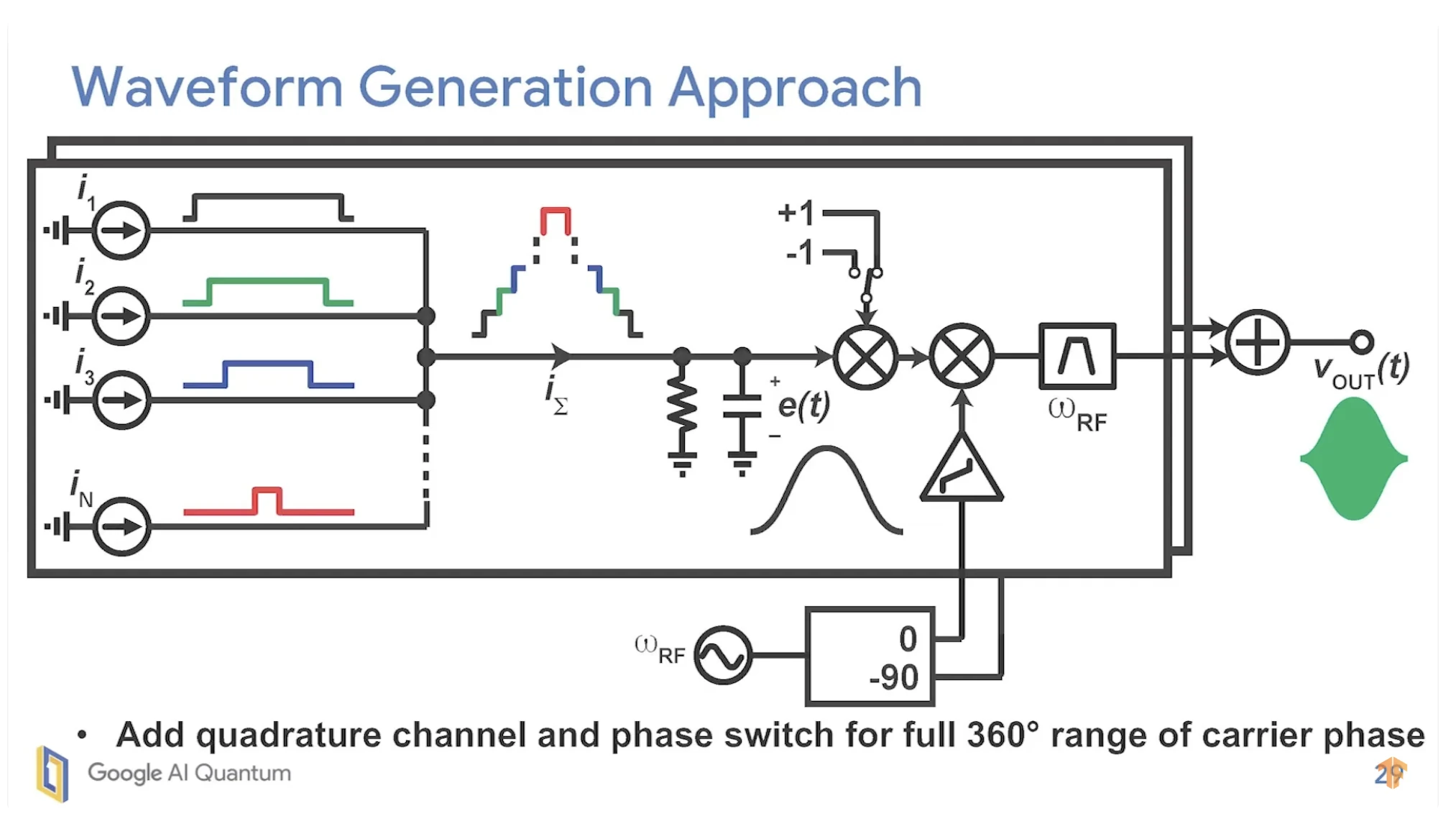
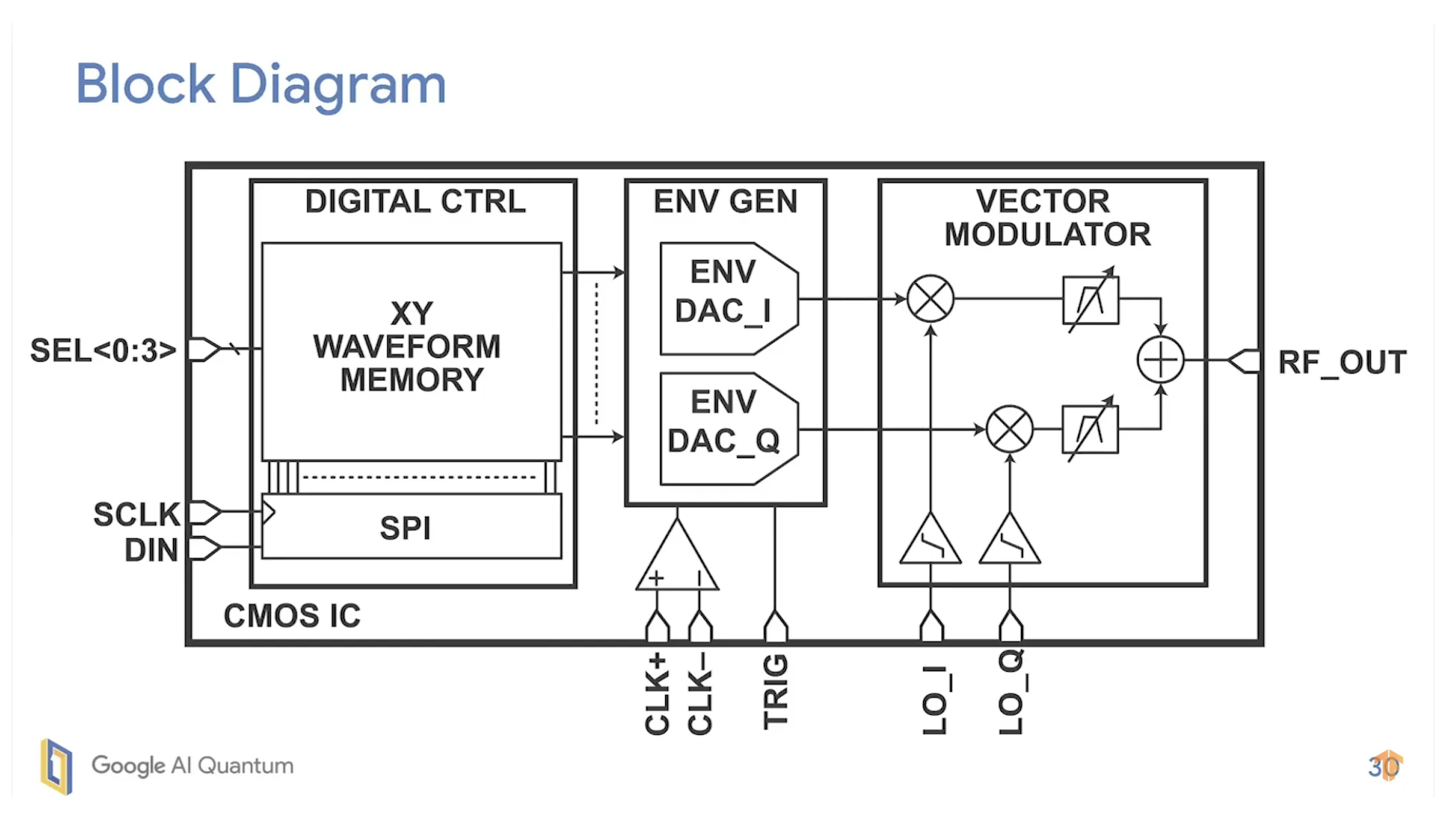
But what does it take to adapat such an architecture to be able to generate a drag pulse? To understand this question, one needs to first understand what a DRAG pulse is.

Mathematical Model Link to heading

A DRAG (Derivative Removal by Adiabatic Gate) pulse is composed by taking a standard Gaussian pulse and adding a scaled derivative of that pulse to its quadrature component. This creates a two-component pulse, with one component being the Gaussian envelope and the other being a Gaussian derivative, which helps to reduce unwanted leakage into higher energy states and correct phase errors in superconducting qubits.

Components of a DRAG pulse Standard Gaussian pulse:

  • The base of the pulse is a standard Gaussian envelope, which is a smooth, bell-shaped curve. This is the “in-phase” \(i(t)\) component of the pulse.
  • Gaussian derivative: A second component is added to the pulse, which is the derivative of the standard Gaussian pulse, scaled by a factor called \(\beta \). This is the “quadrature” \(q(t)\) component.
  • Total pulse: The final DRAG pulse is a combination of these two components \(v(t)\). 
\[ DRAG(t) = v(t)=i(t)+q(t) = i(t)+ \beta \frac{d(i(t))}{dt} \]

There is nothing fancy here, but we need to pay attention that there can many types of DRAG Pulses, and that, even if the standard DRAG Pulse is a Guassian DRAG Pulse, nothing prevents us from having even more powerfull compositions:

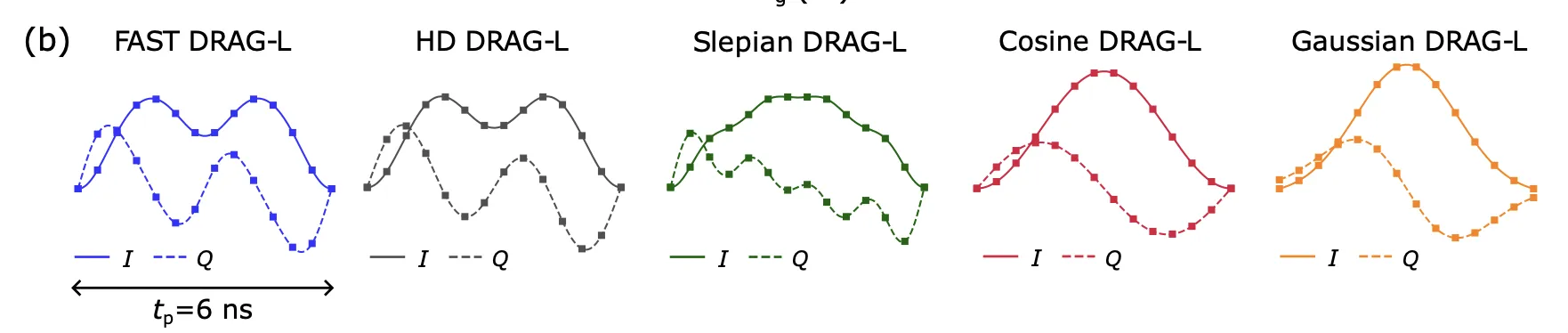Many drag pulse types Credit: APS

Programmatic Model Link to heading

Now that we understand how a DRAG pulse is built, we can examine its implementation with the Quantum Control System. In this case, I will be examining the Qblox Scheduler, which serves as a high-level compiler, enabling users to define experiments in terms of qubits and pulses while abstracting away the complexities of lower-level instrument control.

The code in question is available on gitlab. The code below is a simplified version of the orignal code:

def drag( t: np.ndarray, G_amp, D_amp, duration: float, nr_sigma: float=4, phase: float=0 ) 
    -> np.ndarray:

    mu = t[0] + duration / 2
    sigma = duration / (2 * nr_sigma)

    # In-phase envelope
    gauss_env = G_amp * np.exp(-(0.5 * ((t - mu) ** 2) / sigma**2))
    # Quadrature envelope
    deriv_gauss_env = -D_amp * (t - mu) / sigma * gauss_env

    # generate pulses
    drag_wave = gauss_env + 1j * deriv_gauss_env

    # Apply phase rotation
    rot_drag_wave = rotate_wave(drag_wave, phase=phase)

    return rot_drag_wave

This is actually pretty straightforward, and the orignal code is even more powerful in terms of functionality. Check the online documentation for more information.

Pulse Controller Model Link to heading

The above code works because it assumes that the underlying hardware runs as an AWG, i.e., that any arbitrary wave can be generated based on a sample buffer. But what if it had to be generated on a “pulsar” (or pulse modulator), defined as some kind of control logic sitting at the 4K cryo stage?

Google’s Pulse Modulator: Gen 1 Link to heading

I believe the reason why Google’s architecture is not suitable for DRAG pulse is that the quadrature component would have to be scaled for both amplitude, by the factor \(\beta\), as well as for duration, with the factor \(\sigma\). I will have to confirm if this is true, but for now, we can assume that the challenge is that the pulsar needs to provide full flexibility in I/Q waveform shaping.

In other words, the point is not that the Google cryo architecture cannot generate DRAG pulses; it may well produce I/Q pulses and achieve control over qubits. However, the “standard DRAG” pulse, as used for the highest-fidelity single-qubit gates, may be suboptimal when using that architecture, unless additional calibration/compensation is performed.

Calibrated Pulse Modulator: Gen 2 Link to heading

Since the video from Google dates back to 2019, we can expect that they have already evolved their system with DRAG pulse shaping capability, which we will refer to as the 2nd generation cryo-pulsars. However, since I have not been able to find any information online about Bardin’s Google’s cryo, we can refer to these two evolutions from other research centers:

  • SPulseGen, aka Succinct Pulse Generator, from Osaka University, Japan
  • DLR, aka Delayed Leakage Reduction, from Delft University, The Netherlands

SPulseGen’s generator is designed to tune pulse parameters (amplitude, timing, shape) rather than just replaying a fixed coarse shape. This flexibility is important for implementing a DRAG component (or a “derivative correction”) even if the waveform is somewhat simplified.

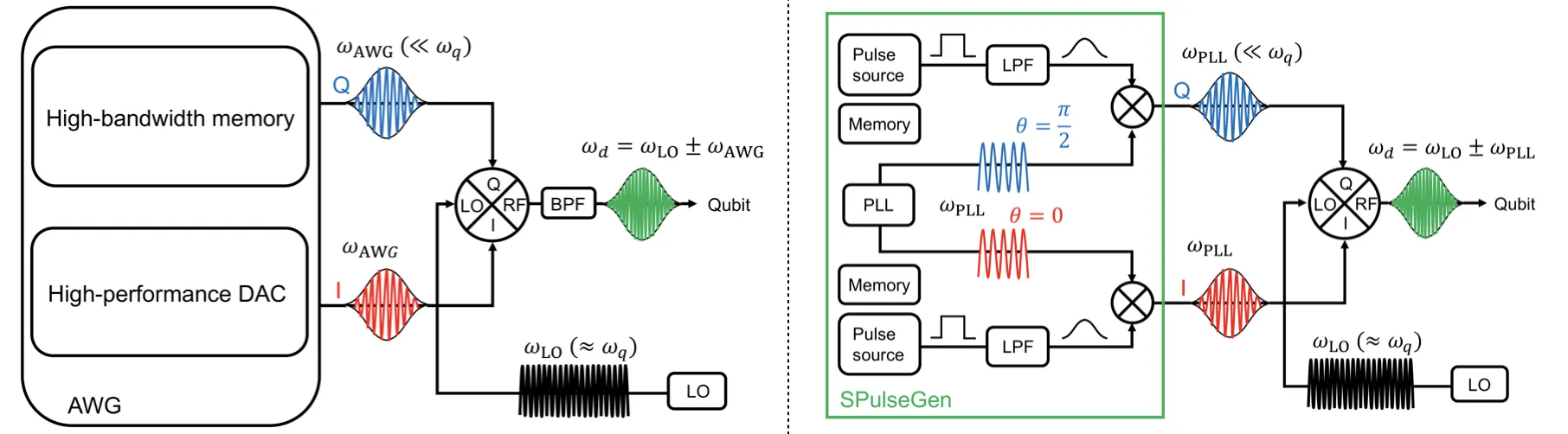
SPulseGen

As for DLR, it sidesteps the requirement of “complex” IQ shaping: instead of needing a continuous derivative quadrature channel, it uses time-delayed repeats of the baseband pulse to generate destructive interference of unwanted (leakage) spectral components.

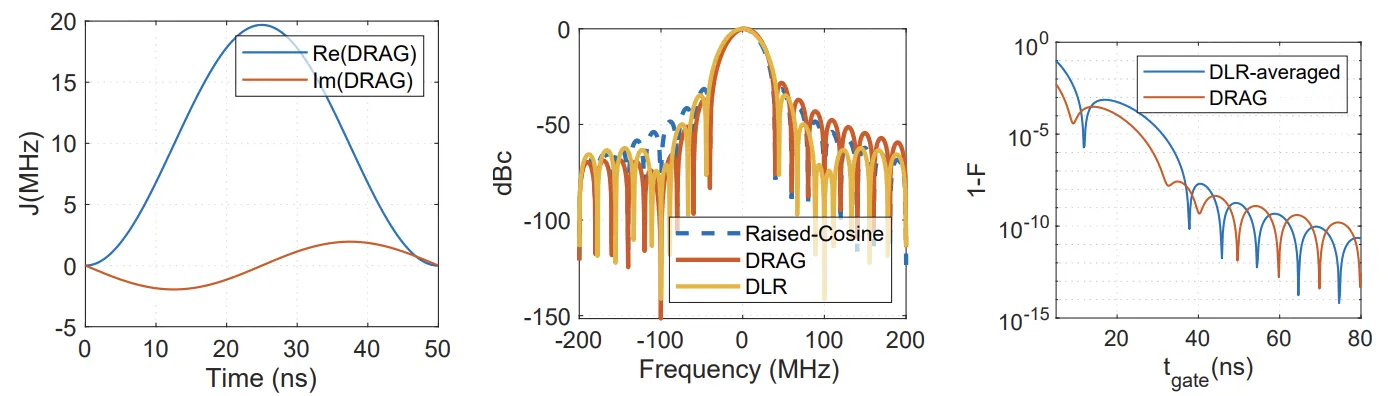
Delayed Leakage Reduction

Both DLR and SPulseGen are designed to address the same high-fidelity and low-leakage control of qubits challenge, all within a context of ultra low power hardware running with Cryo constraints, but with an opposite direction approach:

  • SPulseGen: keeps DRAG and makes it cheaper and smaller to generate.
  • DLR: drops the need for DRAG’s hardware (I/Q modulation) by inventing a new way to achieve the same spectral leakage suppression through temporal interference.

Conclusion Link to heading

Voila, this saturday mind-mapping memo helped me to understand more about the DRAG pulse. From a control logic perspective at the 4K stage, shaping these pulses is not something to worry about.

The challenge nowadays is to learn the optimal calibration and compensation that produces the highest fidelity. Approaches like Delayed Leakage Reduction from TU Delft will definitely make a difference.

An even more interesting challenge is when calibration needs to happen continuously, such as with neural network-based reinforcement learning (RL). It raises the question of whether the neural network should/could/would run at the 4K cryo stage, maybe using in-situ characterization methods.

Meanwhile there are many new developments in ultra-low-power AI ASICs, like blumind.ai, that will make a difference. But let’s keep this investigation of alternative IC architectures for a future memo.

Exciting times, isn’t it?

References