Quantum error correction, also known as QEC, is one of the most active areas of research in quantum computing today. The objective for QEC is to protect the fragile quantum information, stored in the qubits, from noise and decoherence.

The measure of reliability for a qubit is based on the error probability, and today’s physical qubits are able to reach the order of magnitude of about 1 error in 10,000 (\(10^{-4}\)) gate operation. However, to be fully efficient, the gate error rate needs to be able to reach at least 1 in 1 billion (\(10^{-9}\)), or even one in one trillion (\(10^{-12}\)).

This memo aims to provide a light and concise guide to understanding QEC from an implementation perspective. The first section provides an overview of the different error correction computation methods required to create Logical Qubits. The second section examines the potential implementation of gate operations on logically corrected qubits. And the last section introduces the Cuda-QEC framework and its programmatic approach to create quantum error correction systems.

What is QEC trying to solve, and how? Link to heading

The challenge for QEC is, at first glance, simple: first detect when an error has happened, and then correct it. Except that this needs to happen without ever measuring or collapsing the qubit quantum states. This is where the concept of entangled ancilla qubits comes into play:

Instead of storing information in a single qubit, QEC encodes one logical qubit across multiple physical qubits, divided into two categories: data qubits and ancillary qubits (also known as measurement qubits). The group of qubits forms an entangled state such that it becomes possible to read out the ancillary qubits without collapsing the data qubit state. In the picture below, the red line shows several possible logical qubit mappings to the physical qubit.

Modus Operandi Link to heading

Let us suppose that we want to error correct a logical qubit, which is encoded into multiple physical qubits. When an error happens, one of the physical qubits might flip, either in the form of a bit-flip (X), or in the form of a phase-flip (Z), or both (Y).

To check for flip, QEC performs periodic syndrome measurements, which involve measuring specific ancilla qubits that interact with the data qubits. The ancilla qubit is first entangled with the data qubit, and then the readout is done. The entanglement is done for a short period, just long enough for the readout to be performed. In the case of Google, this entanglement is achieved using CZ (control-Z) gates, which, in turn, also utilize entanglement.

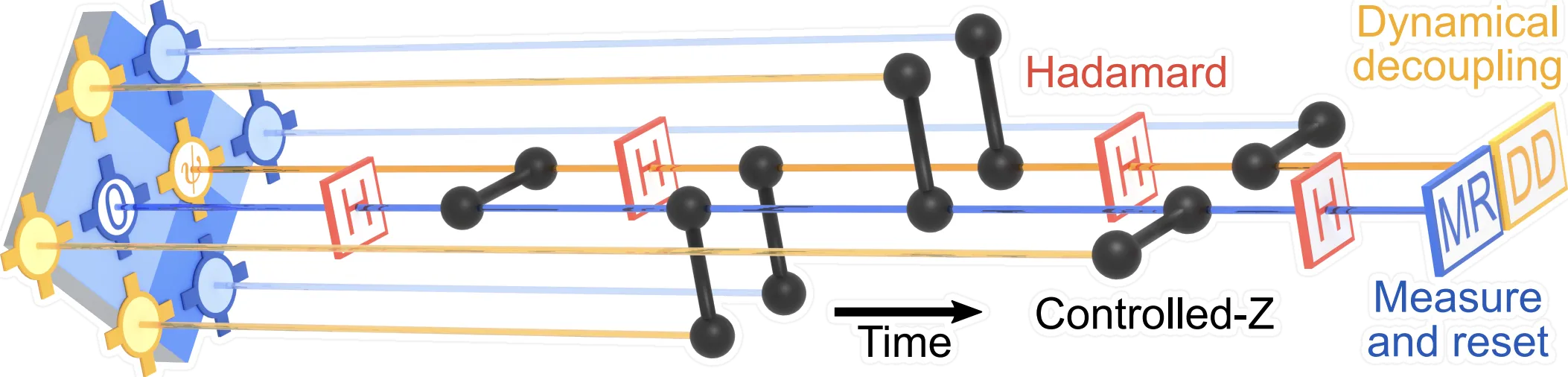Ancilla Qubit measurement> (image source: Google Quantum AI - Implementing surface code logical qubits)

Once the syndromes have been obtained, the correction can be performed; for this, a classical algorithm determines the likely error that has occurred. The system then applies the relevant correction (X,Y, or Z gate). In the case of Google, an additional dynamic decoupling (DD) is used to mitigate dephasing (T2?) errors.

Quantum Codes Link to heading

The data and measurement qubits are distributed non-locally, in a way where an error on one or two qubits doesn’t destroy the group consistency. This distribution is referred to as a quantum code. Real systems use larger, more sophisticated codes:

Shor code (9 qubits): corrects both bit-flip and phase-flip errors.
Steane code (7 qubits): first fully quantum error-correcting code.
Surface codes (\(2n^2-1\) qubits)— It arranges qubits on a 2D grid. The surface code distance \(n\) refers to how many errors can be corrected at the same time

In practice, each measurement qubit is responsible for projectively measuring a stabilizer operator, which is used for the decision logic of the classical algorithm. A stabilizer code is the quantum generalization of linear codes in classical error correction, which uses parity checks to detect errors on noise bits.

How to execute quantum algorithm on logical Qubits? Link to heading

Executing a quantum algorithm on physical qubits means operating gates on physical qubits. But what about when addressing logical qubits? This may seem like a simple question, but the answer is not that straightforward, and there are multiple ways to approach logical qubit gates. Let’s first start with single-qubit gates, and later tackle the multi-qubit gate challenge.

Applying Single-Qubit Gates to Logical Qubits Link to heading

Types of Logical Gate Implementations:

transversal gates: A transversal gate acts independently on each physical qubit.
A logical qubit gate is equivalent to applying the same gate to each of the 𝑛 physical qubits. For example, with the 7-qubit Steane code, a logical Hadamard gate is implemented by applying a physical H gate to each of the 7 physical qubits.
Lattice Surgery / Topological Codes
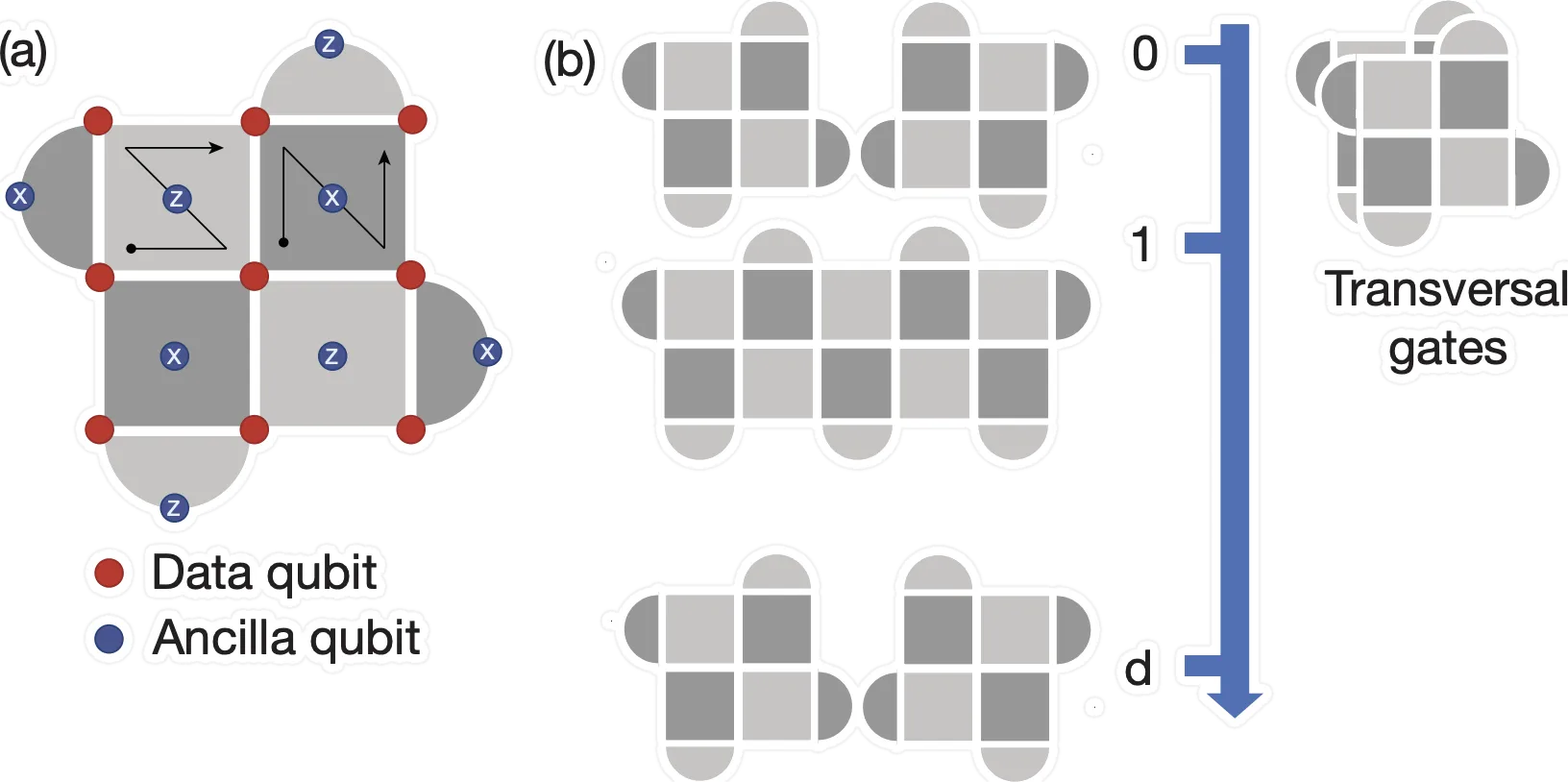
In surface codes, logical qubits are encoded as large patches of physical qubits. Logical operations are implemented by merging and splitting patches or braiding defects, which changes the code topology.
The image on the right from arxiv.2505.15907 shows a lattice surgery operation is performed by joining two code patches along the edge. This operation requires O(d) rounds to achieve fault tolerance.

Applying Multi-Qubit Gates to Logical Qubits Link to heading

Transversal Multi-Qubit Gates: Many of the quantum codes (e.g., Steane, Bacon–Shor), logical CNOT can be done transversally: \( CNOT_L=\sum_{i=1}^n CNOT(a_i,b_i) \)
That is, for every physical qubit \(a_i\) in the control block, apply a physical CNOT to the corresponding qubit \( b_i \) in the target block.
Ancilla-Based Multi-Qubit Logical Gates: When a transversal implementation is not possible, multi-logical-qubit gates can be done via ancilla qubits and teleportation circuits.
For example, the CCNOT (Toffoli) gate cannot be implemented transversally in most codes (*). Instead, it is implemented by creating magic states, which are conditionally “teleported” states, e.g., with a CNOT. Note that in that case, the teleporting gate is a logical gate operation.
Multi-Logical-Qubit Gates in Surface Codes: In topological codes like the surface code, multi qubits gates are implemented differently depending on the gate.
For example CNOT via Lattice Surgery and CZ via Braiding.

Recap Link to heading

Applying multi-qubit gates to logical qubits is done by operating on their encoded physical qubits according to the code’s structure:

Transversal: Pairwise gates between physical qubits of logical blocks.
Ancilla-based: Use teleportation or magic-state methods.
Topological: Perform geometric operations like braiding or lattice surgery.

I need to appologize to the reader that may have been courageous to read up to this pount: this section is a bit light, and way too close to the surface, rather than a deep dive. What one needs to know for now is that there is not a single solution to the single/multi-qubit gate of a logical qubit, but a set of recipes that can be applied for each gate and quantum code types.

Programmatic approach: The Cuda-QX QEC framework Link to heading

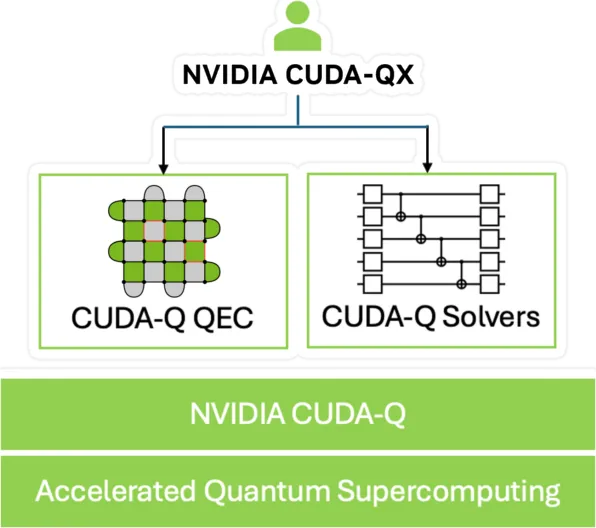
Back in 2024, the Quntum team at Nvidia introduced the CUDA-QX, as an extension of the open-source CUDA-Q platform, providing optimized libraries for quantum developers. Two of the libraries included in CUDA-QX are CUDA-Q QEC (quantum error correction primitives & decoders) and CUDA-Q Solvers (VQE/ADAPT-VQE, QAOA helpers).

Let’s have a quick look at their approach to expose a programmatic API for the custom implementation of the classical logic of the stabilizer operator. Below is a minimal example that implements the simplest decoder, used to detect single-qubit bit-flip errors. The decoder works by checking whether the syndrome matches a single column of the parity matrix Hz, in which case the qubit is detected as flipped:

import cudaq_qec as qec

def run_simple_code_capacity( nShots=1000, errorProbability=0.1 ):
    
    steane = qec.get_code("steane")         # get built-in Steane code from CUDA-Q QEC
    parity_check_matrix = steane.get_parity_z()              # parity-check matrix for Z (bit-flip) errors
    observable = steane.get_observables_z() # Get the Pauli Z observables of the code

    decoder = MyCustomDecoder(Hz) # instantiate custom decoder

    nLogicalErrors = 0
    for _ in range(nShots):
        # Generate noisy data
        data = qec.generate_random_bit_flips(Hz.shape[1], errorProbability) 
        
        # Calculate which syndromes are flagged.
        syndrome = (parity_check_matrix @ data) % 2

        # Decode the syndrome to predict what happened to the data
        result = decoder.decode(syndrome)
        data_prediction = np.array(result.result, dtype=np.uint8)

        # See if this prediction flipped the observable
        predicted_observable = (observable @ data_prediction) % 2
        
        # See if the observable was actually flipped
        actual_observable = observable @ data % 2
        if (predicted_observable != actual_observable):
            nLogicalErrors += 1

    return nLogicalErrors

The important part in the above algorithm is that the parity matrix and predicted observables are obtained from the predefined stean quantum code. A simple decoder can then be implemented this way:

class SingleColumnMatchDecoder:
    def __init__(self, Hz):  # Hz is a parity-check matrix shape (nChecks, nDataQubits)
        self.Hz = np.array(Hz) % 2
        self.n_qubits = self.Hz.shape[1]

    class SimpleDecoderResult:
        def __init__(self):
            self.result = np.zeros(self.n_qubits, dtype=np.uint8)
        def flipped(self, q):
            self.result[q]=1
            return self

    def decode(self, syndrome):
        # ensure syndrome is 1D numpy array of length nChecks
        s = np.asarray(syndrome).flatten() % 2

        # Initialize the flip prediction list
        prediction = SimpleDecoderResult()

        # Compare to each column of Hz: if any column equals the syndrome, pick that qubit
        for q in range(self.n_qubits):
            col = self.Hz[:, q] % 2
            if np.array_equal(col, s):
                return prediction.flipped(q)

        # no single-column match -> predict no flips (all zeros)
        return prediction

With the decoder in place, it is now possible to run the algorithm.

nShots = 1000
nLogicalErrors = run_simple_code_capacity(nShots)
print(f"Shots = {nShots}, Logical error rate ≈ {nLogicalErrors/nShots:.4f}")

As one can see, the Cuda QEC is essentially driven by providing efficient tools and libraries to implement the classical computation logic of the QEC. The question that remains is how this Cuda QEC can get connected to a real quantum stack, and especially how the syndromes are communicated from the control stack to the QEC decoder, and how the decoders inform the control stack, in return, of the corrective gates to be applied. That’s where the fascinating Cuda-Q framework comes into play, but I’ll keep this investigation for a future memo!

Conclusion Link to heading

Voilà, it is clear that delving deeply into the world of Quantum Error Correction is a full-time job, so I will need to stay at a rather high level to maintain momentum in the quantum computing machine architecture. For now, I wonder if I should say a “logically correct” quantum computing machine, or just a “reliable quantum computing machine”? In the first case, the emphasis is on the model that makes the machine correct, while in the second, the emphasis is on the behavior.

It is also unclear to me, as mentioned in a previous post, whether the QEC should be applied as a decoration to the quantum algorithm, meaning that the compiler in charge of translating the quantum gate sequence into something actionable by the control stack is also responsible for “inlining” the gate operations to get the surface code readout. Or whether it should be done as a “background” operation of the “reliable quantum computing machine”?

Notes Link to heading

If you wonder whether one should use Ancillary or Auxiliary, then the right word is Ancillary (Latin ancilla: maidservant), whose meaning is to “provide necessary support to a primary function, while Auxiliary (Latin auxilium: help), meaning is to “provide additional help or reserve support.”.

This note has been added after the initial memo was written:

There is an interesting tutorial about “Tightly integrating GPUs and QPUs for Quantum Error Correction and Optimal Control” from IEEE QCE24, with a video recording available here, that seems to be giving many answers and insights to the above open questions. I will process this tutorial in a future memo. For now, the idea is that a ciruit can be rewritten to fit a given quantum code, lowered to fit a surface-level topology, and post-processed for gates that allow it (clifford gates).

Shor Algorithm combined with QEC

References Link to heading