Raph Levien is famously known for its ultra-efficient implementation of the fastest glyph rendering engine, using a very clever Rust-based SIMD design. His work really inspired me when I was designing an SIMD GPU at Bestechnics in 2023. Later, Ralf Levien also worked on a GPU version of this glyph rendering.
So, when I stumbled on his latests talk about the “How Rust won: the quest for performant, reliable software”, I just decided to focus one hour my time to watch the talk and grab any insight worth learning.

Problem Statement Link to heading
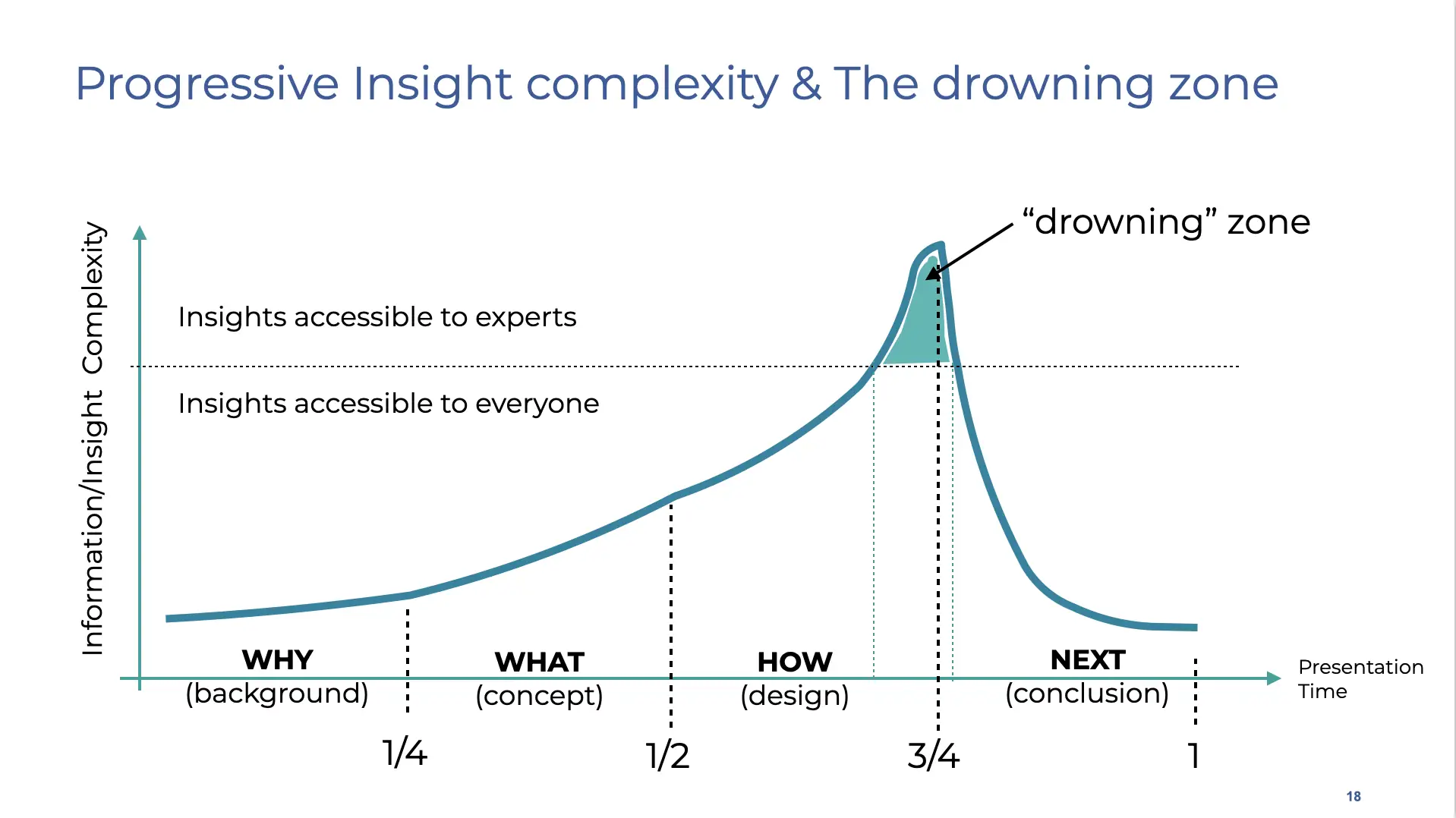
The intense part (also known as the drowning zone) starts around 55:00, with a slide titled Rust secret sauce: more precise type.
At 56:50, Raph says “This is where the affine type comes into play; you want to model (the clonability) as ‘one instance of this exists’; and the type allows you to carefully specify, in the function signature, how that ownership is going to be handled; And I’ll skip over the last example, but it’s fun right…”
I absolutely do not pretend to be a Rust expert, and I admit to have a slight preference for Go - so, the question is, can I make sense of what the affine type really means? And can it be explained with plain words without having to drown in an ocean of knowledge?
Another question, which is pointed out in the YouTube comments: apparently, the return type for the last function should be Cow<'a, [T]> instead of Cow<&'a [T]>. Honestly, this looks even more complicated to me than quantum algorithms. But maybe this does not have to be!
So let’s take a closer look at these ‘more precise type secret sauce’ examples:
fn α( l: &[T] ) → Vec<T>: always allocates, input unaffectedfn β( l: Vec<T> ) → Vec<T>: consumes the input and reuses the allocation.fn δ( l: &mut Vec<T> ): no allocation, just mutates the input vectorfn ω( l: &’a [T]) → Cow<’a,[T]>: might allocate; avoid allocation if duplicates only at ends
First Challenge: Generics Link to heading
The first issue to be checked in the generic template T? Is it really working? Can those functions be compiled as such? Let’s give it a try with the simplest version of the function:
// fails with: error cannot find type T in this scope
fn α( l: &[T] ) -> Vec<T> { vec![] }This obviously does not work, and fails with the error cannot find type T in this scope. If you are familiar with C++, you would anticipate that the type T has to be declared with the function name, so declaring α<T> instead of α.
// all right with the T declaration
fn α<T>( l: &[T] ) -> Vec<T> { vec![] }That works fine this way! But when adding a basic implementation (which only converts to vec, without removing the duplicates), then the compiler fails with the trait bound T: Clone is not satisfied
// fails with: the trait bound `T: Clone` is not satisfied
fn α<T>( l: &[T] ) -> Vec<T> { l.to_vec() }Fortuantely, Rust has a very good documentation on the generic and traits, and after a 10 minute read, it become obvious that we need to change the α<T> to α<T: Clone> as a mean to express the trait bound of type T.
// all right with the trait bound
fn α<T: Clone>( l: &[T] ) -> Vec<T> { l.to_vec() }The next step is to implement a solution to remove duplicates. For this, one approach is to use a HashSet. First, the array is converted into an iterator (let iterator: std::slice::Iter<T> = l.iter();), and we then build a hash set from this iterator (HashSet::from_iter(iterator)), and finally convert the hashset to a vector set.into_iter().collect().
//Fails with: the trait bound `T: Eq` is not satisfied
use std::collections::HashSet;
fn α<T: Clone>( l: &[T] ) -> Vec<T> {
let array_iterator: std::slice::Iter<T> = l.iter();
let hash_set: HashSet<&T> = HashSet::from_iter(array_iterator);
hash_set.into_iter().collect()
}Without any surprise, this fails! And that’s normal, because if you spent the 10 minutes reading the Rust trait documentation, you would know that the HashSet is likely requiring something that can “compare” the elements of type T. This is what the Eq trait does - so, let’s just add it to the trait bound (from α<T: Clone> to α<T: Clone + Eq>):
//Fails with: the trait bound `T: Hash` is not satisfied
use std::collections::HashSet;
fn α<T: Clone + Eq>( l: &[T] ) -> Vec<T> {
let array_iterator: std::slice::Iter<T> = l.iter();
let hash_set: HashSet<&T> = HashSet::from_iter(array_iterator);
hash_set.into_iter().collect()
}It still fails, and the reason is that we forgot to mention that the type T needs to be able to be converted to a hash value. This is what the Hash trait does. So, let change from α<T: Clone + Eq> to α<T: Clone + Eq + Hash>
//Fails with: a value of type `Vec<T>` cannot be built from an iterator over elements of type `&T`
use std::collections::HashSet;
fn α<T: Clone + Eq + std::hash::Hash>( l: &[T] ) -> Vec<T> {
let array_iterator: std::slice::Iter<T> = l.iter();
let hash_set: HashSet<&T> = HashSet::from_iter(array_iterator);
hash_set.into_iter().collect()
}This is where the interesting part of the clonability fun steps in: the hash set is a structure that contains pointers to the elements that were initially in the list, and that were passed by value (to be precise, the array was passed by pointer, and the array contained elements referenced by value). So, we need to tell the hash set to make a copy of those elements, which can be done by adding the cloned() before the last collect (the collect is used to transform the iterator into a vector collection).
// all right!
use std::collections::HashSet;
fn α<T: Clone + Eq + std::hash::Hash>( l: &[T] ) -> Vec<T> {
let array_iterator: std::slice::Iter<T> = l.iter();
let hash_set: HashSet<&T> = HashSet::from_iter(array_iterator);
hash_set.into_iter().cloned().collect()
}And voila, we are ready with the first function example:
fn main() {
println!("{:?}", α(&["A","A","B","D"]));
println!("{:?}", α(&[1,1,2,4]));
}Honestly, this is both complex and not complex. Complex because the compiler enforces strict rules, which have to be declared explicitly rather than derived implicitly, and that makes the learning curve stiff. Not complex, because once you have spent the “10 minutes” reading the doc, well, it should be easier. Perhaps the issue is not that it takes 10 minutes to read the document, but rather that it takes 10 hours to comprehend what is written. This is a feeling of deja vu…
Second Challenge: Affine Type Link to heading
I still have one question about the clonability. Could we return a vector that contains only references to the elements that were passed in the array? At first glance, one would just need to change Vec<T> to Vec<&T> … and properly handle the affine type constraints? Let’s give it a try:
// All right - works fine
use std::collections::HashSet;
fn α<T: Clone + Eq + std::hash::Hash>( l: &[T] ) -> Vec<&T> {
let array_iterator: std::slice::Iter<T> = l.iter();
let hash_set: HashSet<&T> = HashSet::from_iter(array_iterator);
hash_set.into_iter().collect()
}Well, that works! And no complaints about the lifetime? I mean, are we not in the case where we are borrowing the elements, so that the lifetime should be checked? Is the issue that our main function is too simple? So, let’s try something more complex:
// fails with expected named lifetime parameter
fn limited_lifetime() -> vec<&str> {
let l = ["A","A","B","D"];
α(&l)
}
fn main() {
let v = limited_lifetime();
println!("{:?}",v);
}This times, it fails: the compiler complains that there is a missing lifetime parameter, so let’s spend those extra 10 minutes reading the Rust documentation about Validating References with Lifetimes. At first glance, we just need to add the ‘a ?
// fais with: mismatched types; expected `&[str]`, found `&[&str; 4]`
fn limited_lifetime<'a>() -> Vec<&'a str> { ... }But no, that does not work. Let’s try to convert the “immutable str” to a dynamic “String”:
// fails with: cannot return value referencing local variable `l`
fn limited_lifetime<'a>() -> Vec<&'a String> {
let l = ["A".into(),"A".into(),"B".into(),"D".into()];
α(&l)
}Ok, this is actually the error we expect - the borrow checker is indeed working. But, so, how can we tell the compiler that we want the ownership of those locally allocated variables to be transferred? To achieve this, we need to inform the compiler that we want the array l to be allocated on the heap. And for this, we do need to use a vec instead of the array.
// this works
fn β<T: Clone + Eq + std::hash::Hash>( l: Vec<T> ) -> Vec<T> {
let hash_set: HashSet<_> = l.into_iter().collect();
hash_set.into_iter().collect()
}
fn limited_lifetime<'a>() -> Vec<&'a str> {
let l2 = vec!["A","B","B","D"];
β(l2)
}
fn main() {
println!("{:?}",limited_lifetime());
}This version actually works because the new β function takes a vector of elements and returns the same element rather than a pointer to them. So, the elements are being cloned. What if, instead, we want the β function to return a pointer to the input elements?
Third Challenge: Clone on Write Link to heading

Remember the Cow in the last omega function?
fn ω( l: &’a [T]) → Cow<&’a [T]>Cow is actually an enum. It can hold either an immutable (borrowed) reference or a mutable clone of the same. For example:
use std::borrow::Cow;
fn trim_input(input: &str) -> Cow<str> {
if input.ends_with(' ') {
Cow::Owned(input.trim_end().to_string())
}
else Cow::Borrowed(input)
}So, do we need to write Cow<'a [T]> or Cow<&’a [T]>? Well, at first glance, since the input is a pointer & with a lifetime ’a to an object of type [T], the output in also a pointer to an object of the same type. The difference being that Cow<> also stands for pointer. So, yes, it does mean that the correct answer should be Cow<'a, [T]>.
fn ω<'a, T>( l: &'a [T]) -> Cow<'a, [T]> where [T]: ToOwned { Cow::Borrowed(l) }The interesting part here is that, in Rust, arrays have a lenght fixed at compile time. So, how could we be, at run time, allocating a new array with a dynamic size? Well, apparently, according to this stack overflow comment it is not possible. Maybe Ralf did mean to be using a vec instead?
fn ωx<'a, T: Clone + Eq + std::hash::Hash>( l: &'a Vec<T>) -> Cow<'a, Vec<T>> {
let hash_set: HashSet<_> = l.into_iter().collect();
if hash_set.len()==l.len() {
return Cow::Borrowed(l);
}
let own_copy = hash_set.into_iter().cloned().collect();
return Cow::Owned(own_copy);
}Digression Link to heading
Honestly, I must admit to myself I have self-drowned on the syntax “fn ω<‘a, T>( l: &‘a [T]) -> Cow<‘a, [T]> where [T]: ToOwned { Cow::Borrowed(l) }”, which ought to just mean “a clone of the same”.
If we consider that &'a T can be rewritten as Ptr<'a,T>, then we can also rewrite the function as:
fn ω<'a, T>( l: Ptr<'a, [T]>) -> Cow<'a, [T]> where [T]: ToOwned { Cow::Borrowed(l) }If we ommit the fact that T is an array, the code above can be rewritten as
fn ω<'a, T: ToOwned>( l: Ptr<'a, T>) -> Cow<'a, T> { Cow::Borrowed(l) }Then what about rerwritting the type as an macro based expression rather than a syntax?
fn ω<'a, T>( l: Ptr<'a, T> ) -> !Cow(l) { Cow::Borrowed(l) }By allowing to rewrite, the !Cow(l) macro can make it implicit that the type T has to be bound to the trait ToOwned. Thinking this way, we could anticipate that 'a and T are generic types that do not need to be specified explicitely when using the Ptr trait.
fn ω( l: Ptr ) -> !Cow(l) { Cow::Borrowed(l) }What is then confusing that we specify both the compile time type and the run-time implementation without any distinction. But maybe that is what rust is actually about?
Conclusion Link to heading
I think that the “secret sauce” from Ralf is something that could take one hour to explain and have its own slide set - not just 3 minutes in a one-hour talk. It would also be worthwhile to have a critical view of it; maybe not everything is so enjoyable in it? Maybe there is a bit of over-engineering that is disengaging quite a few developers? And maybe this is what is meant by the “fun” of it? Anyway, I’ll try to work on a few slides for a one-hour talk during the next weeks.
Back to the quantum computing challenge - the question is whether we need to have a similar level of complexity to get quantum computing systems to work? Maybe this is the challenge nowadays? Although apparently complex, the quantum algorithms are quite simple compared to this barbarian rust syntax. Maybe we do need to think one step ahead to solve the quantum computing “usefulness” challenge? And that, without this added complexity, we will still only be able to do basic computations?
Assuming that this is all about the semantics of the objects we want to manipulate, perhaps we need to realize that there is a logical abstraction level above the qubits, which is not yet apparent because the industry is still struggling to get qubits to behave.