Using AI, or more precisely Neural Networks (NN), is not only obvious but also an almost mandatory part of any system in 2025. Not surprisingly, numerous research papers have been published on this topic. However, the most recent research has taken the boundaries to the next level by enabling the highly performant integration of neural networks within the Quantum Control system.

I am basing this article on the work from the Singapore Centre for Quantum Technologies CQT/NUS, and more specifically on the research by Arthur Strauss, with whom I had the great honor to discuss and exchange ideas during the last SQA event.

Reinforcement Learning to the rescue Link to heading

Their idea is fascinating: Using a Reinforcement Learning approach to help the quantum control system tune the qubit control (aka gates), based on a system of rewards that aims at maximizing the efficiency of the control. You may ask why this matters. Well, as explained in the previous article (link), qubits are quite sensitive “entities” that require careful attention. And this is where the neural network comes into play, by helping to quantify the quality of this attention, which is sometimes also referred to as fidelity.

How does this work? The reinforcement learning is based on a cycle of Observation/Actions that are learnt via an iterative Environment -> Agent reward system (“a” on the diagram below), usually run with a GPU, and then, once learnt, executed on a tightly coupled matmul (or not!) on the quantum control system (“b” on the diagram below).

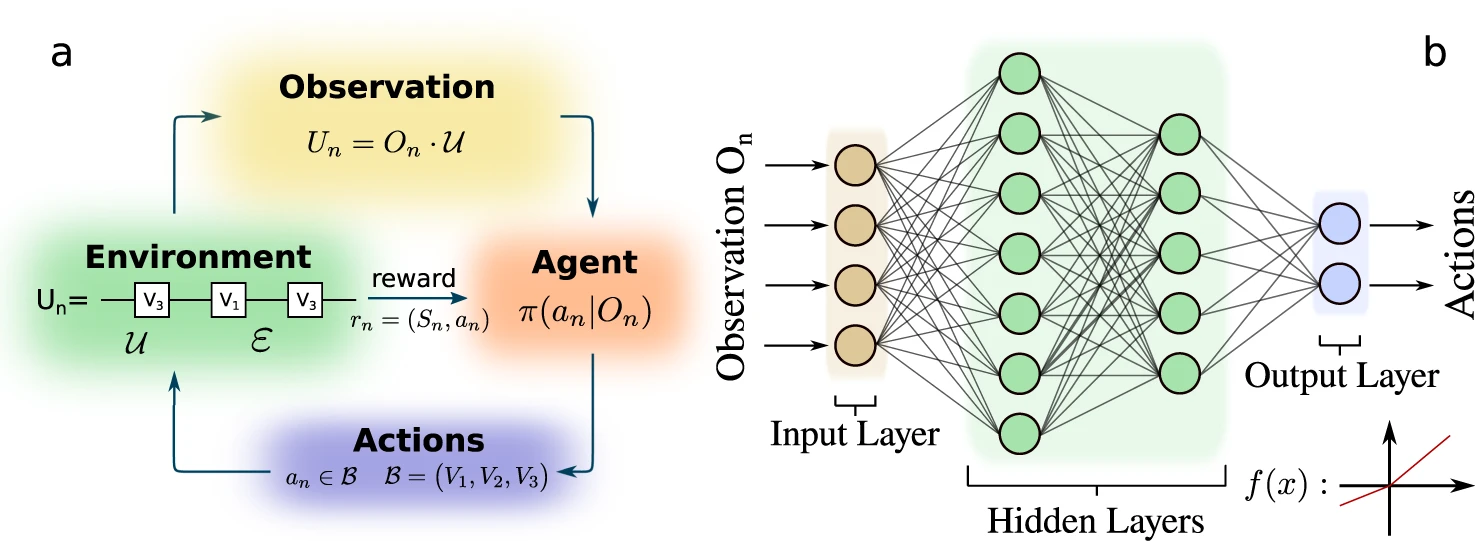Spin Qubits and Quantum Dot Circuits Credits: Nature

Note that since the observation (also called qubit read-out) destroys the quantum state, the learning cycle first resets the qubit state, performs a control gate, reads out the qubit state, and feeds the information to the agent.

RL Systems: Key Components Link to heading

Let’s have a look at the 4 components of the reinforcement learning in detail:

The environment is the quantum controller and qubit itself.
The actions are adjusting the different “knobs” or pulse parameters of the RF generator engine.
The observation is the qubit characteristics after having been manipulated by the environment.
The agent is the one that learns the policy that reacts to the qubit’s observed characteristics and adapts the pulse parameters accordingly.

RL Systems: Learning Methods Link to heading

RL methods can generally be classified into two broad categories: value-based and policy gradient-based.

Value-based methods focus on estimating a value function and deriving policies from it. Policy-gradient methods directly optimize the policy by maximizing the expected cumulative reward through gradient ascent.

The advantage of policy iteration is that it converges much faster than value based, although computational more expensive. And that’s where the policy gradient algorithms come into play, by reducing the computation complexity. Example of policy gradient algorithms, including the reinforce algorithm:

In the above diagrams, s stands for the state, a for action, and r for reward.

RL Systems: Iteration vs Episodes Link to heading

In reinforcement learning, an episode and an iteration are different concepts:

Episode:
- An episode is a complete sequence of interactions between the agent and the environment, starting from an initial state and ending at a terminal state (or after a maximum time horizon).
- Example: In a game of chess, one episode is a full game — from the starting board until checkmate, draw, or resignation.
Iteration:
- In some papers/code, one iteration may mean one time step of agent–environment interaction (state → action → reward → next state).
- In optimization contexts, one iteration may mean one update step of the learning algorithm (e.g., one gradient descent step, which might be based on multiple episodes or transitions).

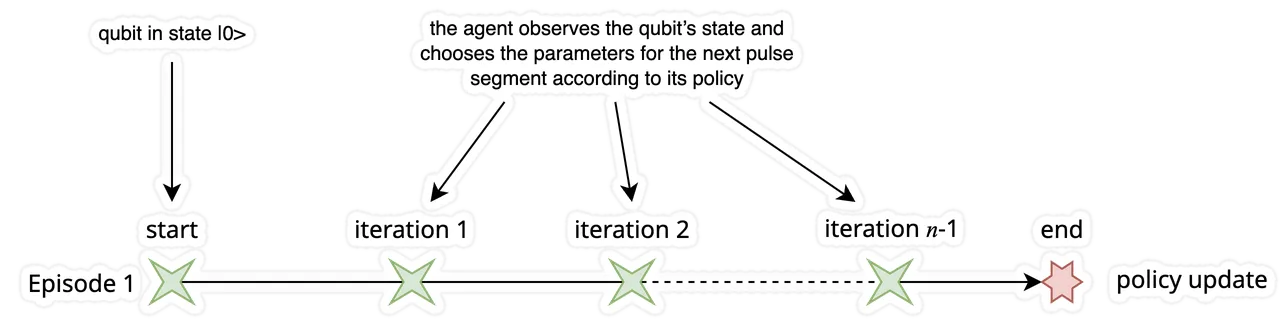
Let’s implement these ideas one by one, starting by the episode sampling.

The episodes start with the qubit in the |O> state.
Start the observe-act loop
- the agent observes the qubit’s state
- and chooses the parameters for the next pulse segment according to its policy.
Explore by sampling the action:
- Instead of deterministically choosing the “best” action (for example the one with highest probability), sampling means that the agent will randomly draw one action from that distribution, according to the probabilities.
- This sampling is essential in the reinforce method.
Compute the score function:
- measure how much more (or less) likely the chosen action becomes if the network parameters are nudged in a particular direction.
- In other words, evaluate ∇(𝜃) for the sampled action.
Compute its reward when the end of the pulse program is reached.

The score and reward, together, drive the learning update in policy-gradient reinforcement learning:

Reward: external feedback from the environment (task performance).
Score: internal sensitivity of the policy to its parameters (gradient of log-probability).

Hands on deep-dive: Flax and Jax Link to heading

to be completed

Conclusion Link to heading

Sorry, that was supposed to be a light-weight blog, and it turns out to be much more complex. Maybe I still need to continue “simplifying the equation”. In any case, what did we learn here? The optimization process for optimally quantifying the quality of the qubits has too many dimensions - and, unsurprisingly, the NNs are very good at solving this challenge. In this blog, we have been focusing on a single-qubit fidelity optimization. But think of two qubits or more: Then you need to learn the impact of the cross-talk. There are many questions and challenges, especially regarding how to learn: globally at the many-qubit level, or locally, and at the qubit pair level. Maybe even hierarchically at the logical qubit level. Many questions, which I’ll be looking at in the next blog about Quantum Error Correction.